我的第一个例子

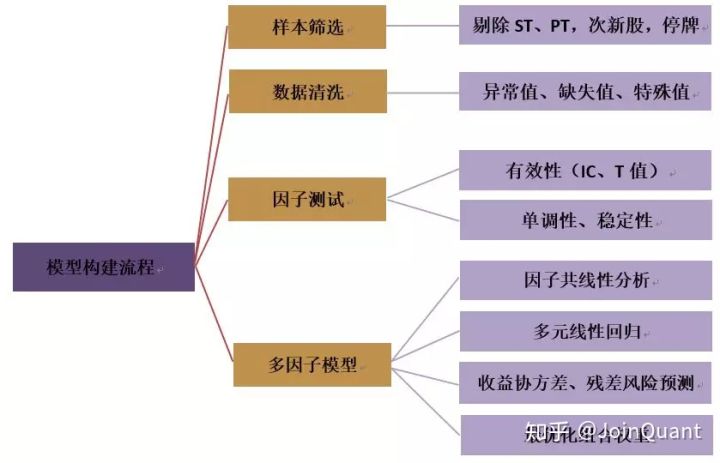
上来先提纲挈领地把各个部分说清楚：

对因子，要验证他的3个性质：

有效性：考察因子是否能够得到持续、稳定的alpha收益，用IC法，看当期因子暴露和下期股票收益的相关性，一般用Spearman；也可以用回归法，T期因子暴露与T+1的股票收益率回归，回归系数为T期的因子收益率，然后考察回归系数的显著性，如果不显著，说明没收益啊。
单调性：用分层法回测，按照因子大小对股票排序，将股票池为N个组合，计算分组累计收益图，看因子单调递增、递减关系。
稳定性：

参考：1，2

确定CLV因子

clv: close location value, ( (close-day_low) - (day_high - close) ) / (day_high - day_low) 这个因子说白了，就是在捕捉每天价格上的变化特征。

构建出因子暴露

因子是一个什么概念呢？它是影响所有股票的共通因素，但是，我们观察上面的CLV，它是每只股票，每天都算一个CLV值出来。

我当时脑子中的一个疑问就是，这不是“共通”的啊，这怎么可能是因子呢？！因子是共通的才对，可是这个值是个股特有的啊。

我的这个以后后来终于解决了？这个玩意确实不叫因子，因子只是个抽象概念，就是表达有那么一种因素，会影响股价。

真正表现出来的东西，叫“因子暴露”，这个才是上面CLV:clv: close location value, ( (close-day_low) - (day_high - close) ) / (day_high - day_low)这个值，用这个值，就是因子的暴露而已。

我们来看这面这个式子，是多因子的对应式子：

$\begin{cases} r_{1t} = \beta_{11}F_1 + \beta_{12}F_2 + ... + \beta_{1k}F_k + \varepsilon_1 \\ r_{2t} = \beta_{21}F_1 + \beta_{22}F_2 + ... + \beta_{2k}F_k + \varepsilon_2 \\ ...\\ r_{nt} = \beta_{n1}F_1 + \beta_{n2}F_2 + ... + \beta_{nk}F_k + \varepsilon_n \\ \end{cases}$ 其中：

$r_{1t}$ 是一只股票的当期收益
$\beta_{11}$ 是当期的，F1因子上的因子暴露
$F_1$ ，是当期的，F1这个因子的收益率
$\varepsilon_1$ ，是当期，无法被因子们解释的收益（残差）
注意！，这个只是一个截面数据，也就是 $t$ 期间的一个股票价格解释

而，我们目前只有一个CLV因子，所以可以简化为：

$\begin{cases} r_{1t} = CLV_{11}F_1 + \varepsilon_1 \\ r_{2t} = CLV_{21}F_1 + \varepsilon_2 \\ ...\\ r_{nt} = CLV_{n1}F_1 + \varepsilon_n \\ \end{cases}$

这里每天的CLV值（每个股票每天，对应一个CLV值），就相当于是上式中的 $CLV_{ij}$ 。

比如你有50只股票，你在2021-1-1，然后你算出50个CLV值，然后你带入上式，

每一行是一只股票，比如这行 $r_{1t} = CLV_{11}F_1 + \varepsilon_1$ ， $r_{1t}$ 就是股票的收益，而CLV_{11}，就是你算出来的CLV因子暴露，而 $F_1$ 才是因子收益率， $F_1$ 才是我们要求的东西！

这里再次强调，我们需要求解的是因子收益率，是共通的。你看上式中， $F_1$ 确实是被各个股票（ $r_{1t},r_{2t},...$ ）共享的。

因子暴露中性化

你好不容易找到一个因子（当然其实不是因子，是因子暴露），但是，市场上其实已经有很多很多因子了，你这个是不是只是它的一个衍生、替身、拷贝？所以，要摆脱其他因子的影子，就要对他进行中性化。

中性化，说白了，就是摆脱对其他因子的影响。

怎么摆脱？最好的办法就是提出它被别的因子线性表达的部分，讲人话，就是用其他因子去线性表示它，然后只留下残差，作为这个因子的真正的中性化以后的因子暴露。

    model = sm.OLS(np.array(tempdata.CLV), np.array(tempdata.MVfactor_std))
    results = model.fit()
    CLVneutralizedfactor = CLVneutralizedfactor.append(pd.DataFrame(results.resid))

看，我们这个例子里，就是用市值因子（MVfactor_std，有个_std后缀是因为做了标准化了），去线性表示CLV，然后，我们留下残差作为新的因子的暴露值（CLVneutralizedfactor）。

这个玩意，就作为将来用作下一步的因子暴露值啦。

常见的中性化处理

一般，都要做两种中性化处理

市值中性化处理，上面已经提到了
行业中性化处理，

看因子和股票的相关性：IC

    corr = pd.DataFrame(neutralized_factor_expose)
    ret = pd.DataFrame(return_5_days)
    corr.columns = ['corr']
    ret.columns = ['ret']
    corr['ret'] = ret['ret']
    ic, p_value = st.spearmanr(corr['corr'], corr['ret'])  # 计算秩相关系数 Rank_IC

要看这个因子暴露，和，股票的收益之间的相关性。

用的是spearman相关，而不是pearson（皮尔逊），两者区别是，pearson直接用2个序列算相关性，而spearman用的是他们每个数在排序的序号来算相关。

这个算完后，看看这个IC值的绝对值的均值，然后还要看平稳性？？？

看因子的收益率

for d in unidate:
    tempdata = combineMatrix1.loc[combineMatrix1['trade_date'] == d, :]
    tempdata = tempdata.dropna()
    model = sm.OLS(np.array(tempdata.FiveDayfwdRtn),np.array(tempdata.CLV))
    results = model.fit()
    CLVFactorRtn.loc[d, 'CLVfactorRtn'] = results.params[0]
    CLVFactorRtn.loc[d, 't_values'] = results.tvalues[0]

用回归法，来计算因子收益率，终于可以算出因子的收益率了，每天算一个收益率出来，每天噢！

然后可以看它的累计收益率了。

分层法

分层法，想证明的就是，看看，是不是因子暴露值大的，收益就应该大？在横截面的一期中，因子收益率对每个股票都是一样的，这个时候，因子暴露值越大，收益率应该也越大。（不对啊，如果因子收益率是负的话，因子暴露值越大，就负的更厉害啊？？？，糊涂了）所以，按照因子暴露值排序后，得到的股票的收益率，可以算一个平均值，然后累加上去，就形成了一个连续的折线图。我们就是要看这个折线图的马太效应，是不是呈现一个扩张、且不相交之势头。扩张意味着，因子暴露值越大，收益越大、或者亏损越大；不相交，说明，因子暴露值对收益的区分度很好，所谓区分度，就是这个收益就是由因子造成的。

这里我有个困惑，如果这个收益累计算的是股票的收益，那股票的收益可能由多个因子作用合成的，所以，我应该只暴露这个股票中属于这个因子的收益率，靠，那不就是因子收益率么？！可是因子收益率是未知的啊，是要靠回归才可以求出的啊？难道，这个收益率是因子收益率？不对，因子收益率对各个股票都是一样的，不可能是它。所以，确实是股票的收益率，按照因子排序后，得到的排序关系，代表综合对因子暴露大小的不同而已，也确实找不到一个很好的只代表这个股票的这个因子造成的收益率的这么一个值，只好用整个股票的收益率代替了。我是这么理解的，就算有其他因子的因素包含在其中，每期都变动股票，每组都好几个股票，其他因子的影响也抵消了吧？

用因子暴露值，对股票进行排序，比如我有50只股票，每一天，我就有50个对某个因子的因子暴露值，我还有50个股票的下一期的预期收益率（注意，是下一期）。

然后，我把这50个股票，按照因子暴露大小排序，用5分位，化成5组，每组10个股票。

然后，我去算这个10个股票下一期的预期回报率的平均（mean）值，

参考

Alpha策略-因子选股

第一个例子