基础概念
你抽样出来得到一个集合(),然后你尝试用这些样本去推断整体的统计特性(比如分布、均值、方差啥的。)
这个抽样集合(),它也是有个分布的呀,它也是一组随机变量的值啊,它也是被看做是一个随机变量(有自己的分布啥的)
然后你用这个集合()构建出一些新的“函数”出来,得到的又是个新的随机变量,这玩意给了个新名字:“统计量”,是的,统计量就是个“随机变量”,所以丫也有概率分布呀。统计量在统计之地位,相当于,随机变量在概率中的地位。
啥意思?我举个例子吧,加入你从全国孩子里抽样孩子们的身高值,抽出1000个孩子,随机的,那,这每个孩子就对应上面说的,这是一次抽样,然后,你可以放回这些孩子,再抽一次,你又得到一组1000个孩子的抽样;然后,你干了一件事,对这两次的抽样,求了一个平均值,这个平均值,就是一个所谓的统计量,对,他就是一个随机变量,它有了2个值(第一次抽样的均值、第二次抽样的均值),然后,这个随机变量,也就个统计量,他也会有有个概率分布,恩,我们就是要研究它的特性。
充分统计量:就是你这些抽样出来的统计量,完全可以代表样本总体,不损失什么信息。
常见的统计量:
- ....
我们后面不讨论一个抽样集合了,而都是讨论这些统计量。
均值统计量
如果是总体分布是正态的,那么样本均值这个统计量,它符合一个正态分布:
注意注意!这里的,都是总体样本的哈。
那你可能会问了,如果总体不是正态分布的咋办?幸运的是,通过中心极限定理的证明,得到结论,样本均值的分布还是,上面这个式子(均值为总体均值,方差为总体方差的的1/n),但是,前提是n得比较大才行,那多大算“比较大”?一般认为是抽样数超过30个。
中心极限定理:
均值为,方差为的总体,抽样n个样本,n足够大的时候,样本均值的抽样分布,近似符合方差为,方差为的正态分布。
注意!
这句话暗藏玄机,不是说你抽样的结果符合正态分布,而是你抽样的样本的均值,符合正太分布,讲人话,就是你抽n个,得到一个均值,然后你又去抽,又得到一个均值,前面说了,这个均值,就是统计量,就是个随机变量。现在说的是,这玩意,这个抽样的的均值,丫符合正态分布,懂了么?敲黑板!是“样本均值“近似正态,不是样本近似正态!所以才叫“中心”极限定理嘛。
另外,你观察这个正态分布的方差是,n是啥?n是抽样的个数,n越大,这个方差越小,也就是,你抽样出来的均值,他离总体样本均值的波动,越来越小。
方差统计量
样本方差的统计量,比较复杂,书上说,它和总体分布有关。
如果总体分布是正态的,他的抽样样本的方差的分布为n-1的卡方分布。(啥是卡方分布,下面会讲)
矩
矩源于物理学中力矩,但是,在统计学里成为衡量一个概率分布的指标。
参考:统计学中矩的理解
| 名称 | 表示形式 | 含义 |
|---|---|---|
| 样本矩 | 近似估计,假设所有情况概率相同。 | |
| 一阶原点矩/期望 | 也称为随机变量的中心,加权均值。 | |
| 二阶原点矩 | ||
| 一阶中心距 | 显然,任何随机变量的一阶中心距都是0。 | |
| 二阶中心距/方差 | 表示该变量离其期望值的离散程度(距离)。平方根叫标准差。 | |
| 三阶中心距/偏态 | 偏度衡量实数随机变量概率分布的不对称性。 | |
| 四阶中心距/峰态 | 峰度高就意味着方差增大是由低频度的大于或小于平均值的极端差值引起的。 |
解释:
- 期望(Expectation): 表示加权平均。
- 方差(Variance): 表示某个样本或变量偏离期望值的程度或者距离。
- 偏态(Skewness): 在概率论和统计学中,偏度衡量实数随机变量概率分布的不对称性。
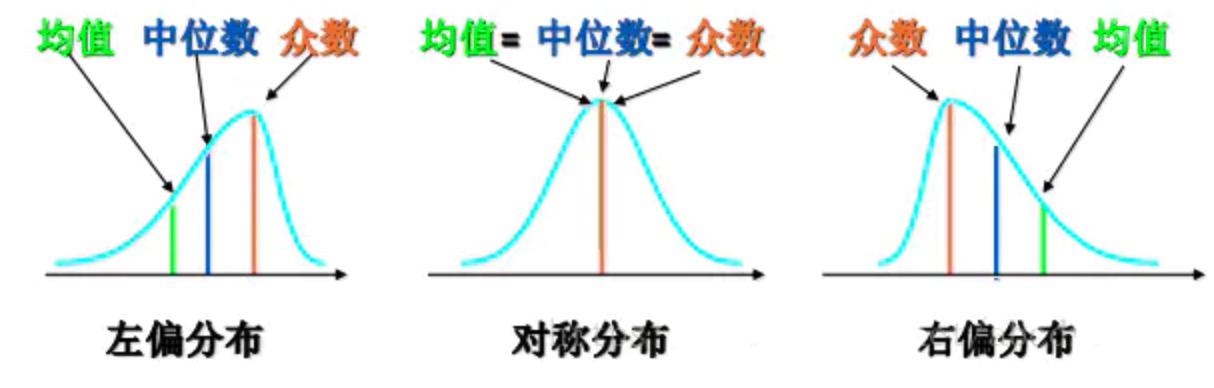
- 偏度<0时,概率分布图左偏
- 偏度=0时,表示数据相对均匀的分布在平均值两侧,不一定是绝对的对称分布
- 偏度>0时,概率分布图右偏
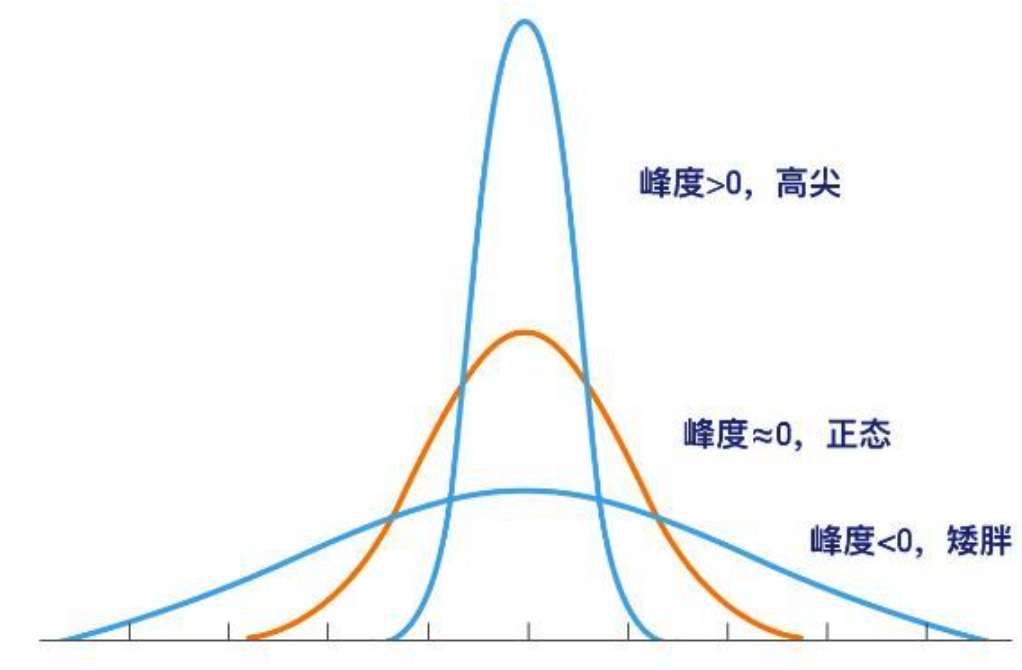
- 峰态(Kurtosis): 在统计学中,峰度高就意味着方差增大是由低频度的大于或小于平均值的极端差值引起的。标准正态分布,峰度=3。(图里标错了)。值越大越尖。