一元回归

一元回归，主要是来用来探讨，数值因变量（$y/f(x)$）和数值自变量$x$之间，是不是有关系，有怎样的关系的一个数学工具。 这里的自变量$x$，只有一个，所以才叫一元回归，多元回归我们下一节讨论。

相关性分析

为了分析变量之间的关系，先提出一些灵魂拷问：

• 变量之间存在关系么？（如果没关系，就不能称之为因变量、自变量啥的了）
• 如果存在关系，是什么关系？（如何用数学刻画出来）
• 这种关系的强弱如何？
• 样本之间反映的关系能代表总体么？（这个其实很重要，毕竟你得到的数据都是抽样数据，你分析抽样数据有关系，就代表总体上也有这种关系么？）

散点图是个好东东，教材给出了示例：

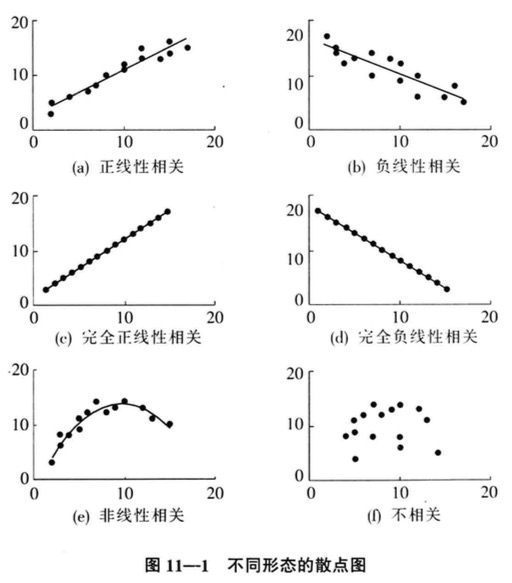
形象化体会后，我们给出数学上的度量方法：

相关系数 correlation coefficient

总体的相关系数记作$\rho$，总体的相关系数记作$r$。

$r=\frac{n \sum x y-\sum x \sum y}{\sqrt{n \sum x^{2}-\left(\sum x\right)^{2}} \cdot \sqrt{n \sum y^{2}-\left(\sum y\right)^{2}}}$

也可以表达成：

$$r=\frac{\sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)\left(Y_{i}-\bar{Y}\right)}{\sqrt{\sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2}} \sqrt{\sum_{i=1}^{n}\left(Y_{i}-\bar{Y}\right)^{2}}}$$

这两种表达是等价的，参考皮尔逊积矩相关系数。

这个公式也称作：线性相关系数、Pearson相关系数

• r的取值范围[-1,1]，0是无关，1是完全正相关，-1是完全负相关
• r只能表示x和y有线性关系，但是给不出具体的线性关系
• r不能反映非线性关系，极端的时候r=0，xy可能都有非线性关系

接下来一个问题，$r$可不是总体的相关性$\rho$，它只是抽样的，那么一个问题是，这个抽样能代表总体么？也就是所谓r的可靠性、显著性。

所以，我们先得琢磨琢磨，这个抽样的相关系数$r$，它是个统计量啦，它也是个随机变量啦，它到底符合什么分布？

教材上没给出推导，只给了结论：

• 当总体是正态分布，随着n的增大，抽样的相关系数$r \to$ 正趋向于态分布。
• 但是，上述仅在总体的相关系数$\rho=0$时候更趋近，但是在$\rho = \pm 1$两头时候，会呈现偏态：$\rho$负值$r$值右偏，$\rho$正值时候$r$左偏

所以，不能用正态分布来估计$r$的分布了，那用啥？用t检验！（至于为何用t检验，教材上也没细说）

这样，假设检验的流程就变成：

• 提出$H_0: \rho = 0 , H_1: \rho \ne 0$
• 计算检验所使用的统计量：$t = \|r\| \sqrt{\frac{n-2}{1-r^2}} \sim t(n-2)$

t分布咋来的来着？X ~ 标准正态分布，Y ~ 卡方分布，那，他们的合体，$𝑡=\frac{𝑋}{\sqrt{𝑌/𝑛}}$ 服从自由度为n的T分布； 而卡方分布，正是一堆正态分布的平方和 这里的t分布咋推出来的？教材上没给出推导，只给了结论。

然后，给定一个显著性水平$\alpha$，算出对应的t，看t的范围，得到是否接受原假设。

回归公式

前面的相关性，只给出了变量间的关系强度度量，但是，我们还需要一个明确的数量关系的描述，这个就需要回归分析了。

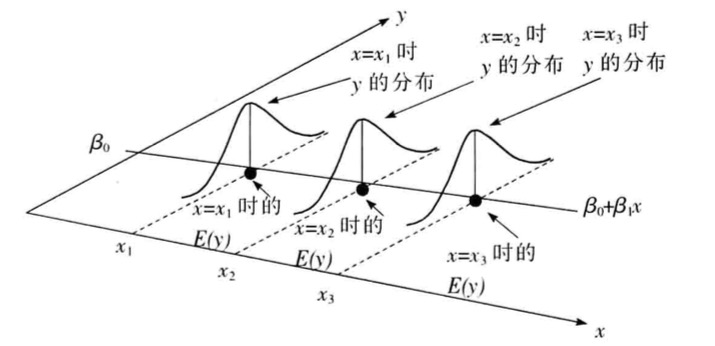
一元回归的表达式：$y = \beta_0 + \beta_1 x + \epsilon$

对这个式子的理解：

• $\beta_0 + \beta_1 x$，是对线性部分的刻画
• 误差项$\epsilon$反应的是线性关系外的随机影响，不能被线性关系解释的变异性，它的期望$E(\epsilon)=0$，服从一个正态分布$\epsilon \sim N(0,\sigma^2)$
• 这个式子，是假定$x,y$是存在线性关系的
• 假定x都是确定值，而回归出来的y是个随机变量，它是$\beta_0 + \beta_1 x$加上一个$\epsilon$扰动项，但是$y$的期望$E(y)=\beta_0 + \beta_1 x$
• 误差项$\epsilon$彼此间不想关，就是$x_1$对应的$\epsilon_1$和$x_2$对应的$\epsilon_2$没有任何关系
• 上句话，也可以表达成，任何$y$都服从均值为$\beta_0+\beta_1$，方差为$\sigma^2$的正态分布

参数估计

一元回归的表达式中，$\beta_0,\beta_1$是未知的，需要我们用数据去估计他们，我们也没法用总体去估计他们，我们只能用抽样的值，去估计他们， 这也就是样本统计量 $\hat{\beta_0},\hat{\beta_1}$（我们始终是在用样本的统计量去估计总体，始终牢记这点），我们就得到了样本回归方程：

$\hat{\y} = \hat{\beta_0} + \hat{\beta_1} x$

然后我们用最小二乘法，得到最优的样本数据对应的$\hat{\beta_0},\hat{\beta_1}$

$\sum\left(y_{i}-\hat{y}_{i}\right)^{2}=\sum\left(y_{i}-\hat{\beta}_{0}-\hat{\beta}_{1} x_{i}\right)^{2}$

也就是求解这个方程的最小值，通过求极值，求偏导，可以得到一个解析解（不推导了，请参考教材）：

$$\left\{\begin{array}{l} \hat{\beta}_{1}=\frac{n \sum_{i=1}^{n} x_{i} y_{i}-\sum_{i=1}^{n} x_{i} \sum_{i=1}^{n} y_{i}}{n \sum_{i=1}^{n} x_{i}^{2}-\left(\sum_{i=1}^{n} x_{i}\right)^{2}} \\ \hat{\beta}_{0}=\bar{y}-\hat{\beta}_{1} \bar{x} \end{array}\right.$$

当然，回归也不用你这么费劲去算，用Excel的“回归统计”功能，或者各种开发语言中的软件包，可以方便求解。

拟合度评价

虽然我们可以拟合出直线，但是，这个直线到底好不好，是不是“完美”或者“很垃圾”地拟合了抽样数据和变量呢？ 我们使用给一个叫判定系数$R^2$的概念:

$R^{2}=\frac{S S R}{S S T}=\frac{\sum\left(\hat{y}_{i}-\bar{y}\right)^{2}}{\sum\left(y_{i}-\bar{y}\right)^{2}}=1-\frac{\sum\left(y_{i}-\hat{y}_{i}\right)^{2}}{\sum\left(y_{i}-\bar{y}\right)^{2}}$

这个式子里SSR、SST啥意思？以及各种表示、意义都必要好好说一下：

先说表示：

• $\hat{y}_i$，就是直线拟合出来的y，就是直线上的点的y
• $\bar{y}$，是所有样本真实y的平均值
• $y_i$，是某个样本的真实y值

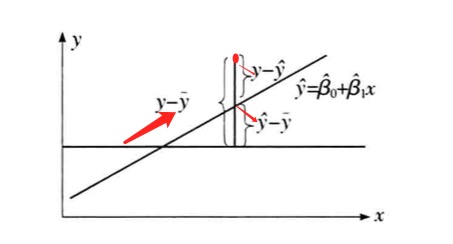
接下里解释含义，先推导：

$$\begin{aligned} \sum\left(y_{i}-\bar{y}\right)^{2} &=\sum\left(y_{i}-\hat{y}_{i}\right)^{2}+\sum\left(\hat{y}_{i}-\bar{y}\right)^{2}+\\ & 2 \sum\left(y_{i}-\hat{y}_{i}\right)\left(\hat{y}_{i}-\bar{y}\right) \\ \because \sum\left(y_{i}-\hat{y}_{i}\right)\left(\hat{y}_{i}-\bar{y}\right) & = 0 \\ \therefore \sum\left(y_{i}-\bar{y}\right)^{2} &=\sum\left(y_{i}-\hat{y}_{i}\right)^{2}+\sum\left(\hat{y}_{i}-\bar{y}\right)^{2} \end{aligned}$$

我们给出上式中各项命名：

总平方和SST : $\sum\left(y_{i}-\bar{y}\right)^{2}$ 残差平方和SSE: $\sum\left(y_{i}-\hat{y}\_{i}\right)^{2}$

回归平方和SSR: $\sum\left(\hat{y}\_{i}-\bar{y}\right)^{2}$

上面的推导结果，就可以表达成： 总平方和SST = 回归平方和SST + 残差平方和SSE

这个式子表达了什么含义呢？

我换个表达：

一个真实y和真实y们的均值的差的平方SST，可以分解成 = 拟合出来的y和真实y们的均值的平方差（这个是说，你用直线拟合出来的部分/值）SSR + 剩下的你拟合不出来的残差们和真实y们的均值的平方差SSE

大白话就是，

总的和基准（真实y的均值）的差距SST = 可以模拟出来的差距SSR + 模拟不出来的差距SSE

然后，我们再看判定系数$R^2$，就迎刃而解了：

判定系数$R^{2}=\frac{SSR}{SST}=\frac{\sum\left(\hat{y}_{i}-\bar{y}\right)^{2}}{\sum\left(y_{i}-\bar{y}\right)^{2}}$

那大白话，就是，可以模拟出来的差距 除以 总差距，判定系数$R^2$越大（约接近1），说明拟合的越好 呗！

这里有个结论，很诡异：

相关系数$r$是判定系数$R^2$的平方根，这俩貌似没啥关系的东西，居然是这么一个关系。相关系数$r$是看x和y的相关性的，$R^2$是度量回归方程拟合程度的， 这俩居然可以相互照应起来。线性回归拟合越好，说明相关性越高，噢！符合直觉啊，赞了。

至于推导，懒得写了，参考这篇把相关系数和R方的关系是什么？。

R2的取值范围是[0，1]。 R2越接近于1，表明回归平方和占总平方和的比例越大，回归直线与各观测点越接近，用x的变化来解释y值变差的部分就越多，回归直线的拟合程度就越好；反之，R2越接近于0，回归直线的拟合程度就越差。

显著性检验

你做了一元回归，人家到底是不是线性关系啊？你是不是应该做假设检验？

除此之外，你还得保证$\hat{\beta}\_1$这个和$x$相乘的系数，也得不为0啊，否则，这就是一条直线了啊。这个也需要假设检验（检验不为零）。

线性回归检验!

检验线性，是通过一个比较复杂的统计量来检验的：$F=\frac{SSR/1}{SSE/(n-2)}=\frac{MSR}{MSE} \~ F(1,n-2)$。

其中：

• SSR: 回归平方和，$\sum\left(\hat{y}_{i}-\bar{y}\right)^{2}$，就是拟合值$\hat{y}$和均值$\bar{y}$的差异，是体现线性关系表达的能力
• SSE: 残差平方，$\sum\left(y_{i}-\hat{y}_{i}\right)^{2}$，他体现你预测的，和真实值之间的差，是线性表达不了的差异。
• MSR: SSR除以自由度（一元回归是1，就是参数数量-1）
• MSE: SSE除以相应自由度（SSE自由度是$n-k-1$）,一元回归k=1，所以是n-2。
• 最后，构建出的统计量$\frac{\sum\left(\hat{y}_{i} - \bar{y}\right)^{2}/1}{\sum\left(y\_{i}-\hat{y}_{i}\right)^{2}/n-2}=\frac{SSR/1}{SSE/(n-2)}=\frac{MSR}{MSE}$，它恰好符合F分布（F分布啥来着来着？是nY/mZ，Y和Z都是$\chi$卡方分布，而卡方分布又是正态分布的平方和的分布；观察这个式子，F分布可能就是如此得出的，我猜）。

终于，我们可以用上述的构建的统计量来做检验了：

1、提出原假设$H_0:\beta_1=0$，也就是线性关系不显著

2、计算统计量$F=\frac{SSR/1}{SSE/(n-2)}=\frac{MSR}{MSE} \~ F(1,n-2)$

3、给出一个显著水平$\alpha$，确定自由度，一个是1，一个是n-2，查表可得临界值$F_\alpha$，如果$F>F_\alpha$，拒绝原假设$H_0$，即线性相关。否则，线性相关不明显，或者说不相关。

回归系数检验

上面是判断线性关系，接下来似乎判断系数$\beta_1$不为0，原因是，它为0，线性相关就没有意义了。

我靠！你发现没有，这怎么和上一个线性相关的检验的标准一样啊，都是$\beta_1\ne 0$啊，其实，是有区别的。区别在于，检验用的统计量不同。这里确实有些诡异，不过，上面那个跟强调检验线性关系，而下面这个重点在于系数不为0，不过我说的自己都心虚，先姑且这样理解吧。

自问自答：我的猜想是对的！上面的F检验和下面的t检验，是一样的，是等价的，当然，这个只对一元回归，多元回归就不行了，原因是多元回归有多个参数了，得一个一个地检验了。

这个统计量为：$t=\frac{\hat{\beta_1} - \beta_1}{s_{\hat{\beta_1}}}$

这个式子怎么来的呢？

首先，教材上说，$\hat{\beta}_1$服从正态分布，标准差为$\sigma_{\hat{\beta1}_1} = \frac{\sigma}{\sqrt{\sum x^2_i - \frac{1}{n}(\sum x_i)^2}}$，$\sigma$是误差项$\epsilon$的标准差，这个不得而知，所有用它对应的估计量$s_e$近似替代，得到估计量的$\hat{\beta}_1$的方差$s_{\hat{\beta}\_1}=\frac{s_e}{\sqrt{\sum x^2_i - \frac{1}{n}(\sum x_i)^2}}$。

其中，$s_e$为抽样的预测$\hat{y}\_i$和真实值$y_i$的误差项$\epsilon$的标准差估计。这里需要解释一下，你用样本估了一条直线，你就得到了一条连续曲线，这条连续上所有的y和总体，总是可以算出所有的误差$\epsilon$的，但是，由于你没法知道这个值，你还得用你的那些样本算一个这些样本对应的$\hat{\epsion}$，这个值其实就是$s_e$。

$$s_{e}=\sqrt{\frac{\sum\left(y_{i}-\hat{y}\_{i}\right)^{2}}{n-2}}=\sqrt{\frac{S S E}{n-2}}=\sqrt{MSE}$$

而这个统计量：$\frac{\hat{\beta_1}-\beta_1}{s_{\hat{\beta_1}}}$，符合自由度为2的t分布。

这样，就可以使用这个统计量做假设检验：

1、提出原假设$H_0:\beta_1=0$，也就是线性关系不显著

2、计算统计量$t=\frac{\hat{\beta_1}-\beta_1}{s_{\hat{\beta_1}}}$

3、给出一个显著水平$\alpha$，自由度是n-2，查表可得临界值$t_{\alpha/2}$，如果$t>t_{\alpha/2}$，拒绝原假设$H_0$，$\beta_1 \ne 0$。否则，接受原假设$\beta_1=0$。

利用回归方程预测

TODO

残差分析

在回归模型$y=\beta_0 + \beta_1 x + \epsilon$中，对$\epsilon$的要求是均值为0，正态分布，方差相等，所以，同归对残差$\epsilon$的检验，可以反向验证你的回归模型正确与否。

所以，可以将残差标准化后，对其进行正态检验。

$z_{e_i} = \frac{e_i}{s_e} = \frac{y_i - \hat{y}\_i}{s_e}$

• $s_e$是残差的标准差估计。